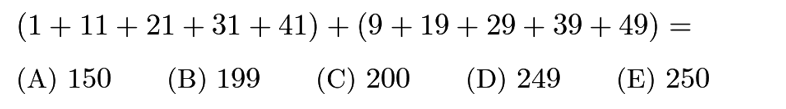
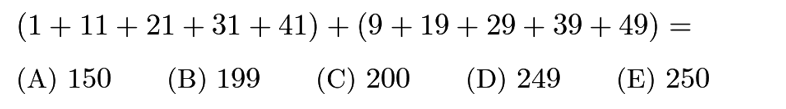
Answer: E
Solution:
=(1+49)+(11+39)+(21+29)+(31+19)+(41+9)=50*5=250.

Answer: D
Solution:
=200/1000+40/1000+6/1000=246/1000=0.246.
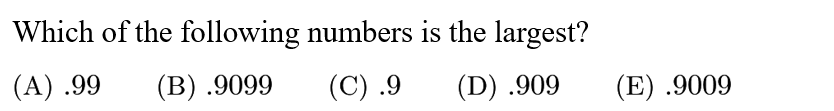
Answer: A
Solution:
We have .99>.9099>.909>.9009>.9, So choice A is the largest.

Answer: E
Solution:
401 is around 400 and 0.205 is round 0.2. So the fraction is approximately 400/0.2=2000.
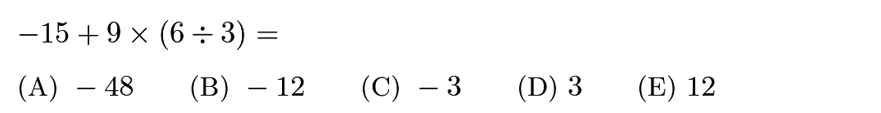
Answer: D
Solution:
=-15+9*2=-15+18=3.
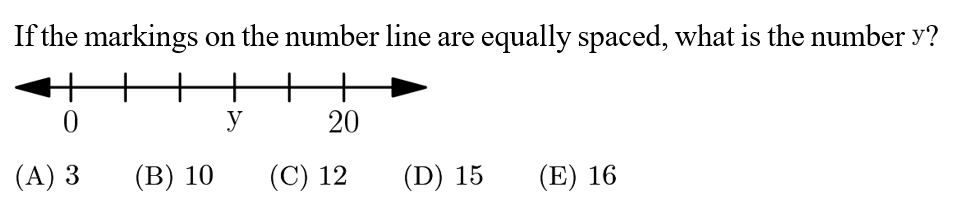
Answer: C
Solution:
Five steps are taken to get from 0 to 20. Each step is of equal size, so each step is 4. Three steps are taken from 0 to y, so y=3*4=12.
Answer: D
Solution:
We have 20*25+10*10=10*25+n*10; => n=35.

Answer: E
Solution:
=24*(6/12+4/12+3/12)=24*13/12=26.
Answer: C
Solution:
Besides ensuring the situation is possible, the 30 students information is irrelevant.
From the first statement, we can deduce that 2 of every 2+3=5 students are boys. Thus, 2/5=40% of the students are boys.

Answer: D
Solution:
The smaller angle makes up 5/12 of the circle which is the clock. A circle is 360, so the measure of the smaller angle is 5/12 * 360=150.
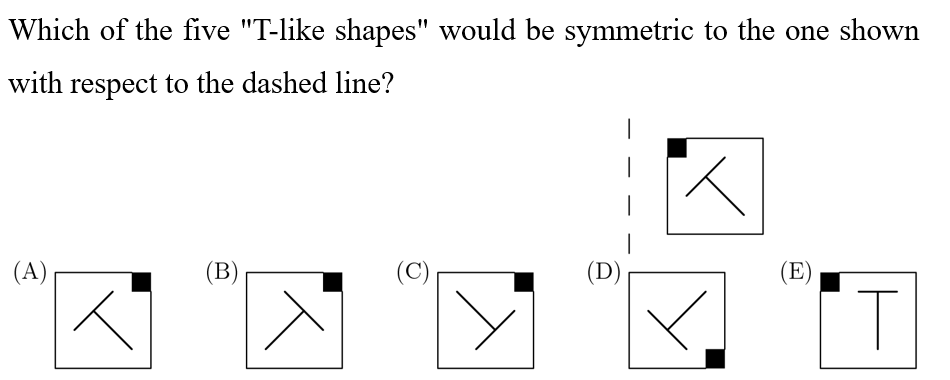
Answer: B
Solution:
Drawing the reflection, we see that it is B. Imagine it as if it were a mirror reflection or if you were to flip it over the dashed line.
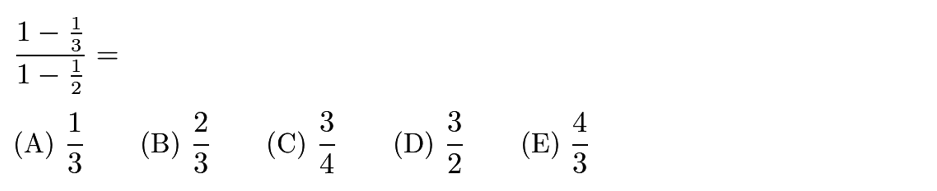
Answer: E
Solution:
=(2/3)/(1/2)=2/3 * 2=4/3

Answer: A
Solution:
9/(7*53)= (0.9*10)/(0.7*10*53) = 0.9/(0.7*53)

Answer: C
Solution:
When trying to minimize a-b, we minimize a and maximize b. Since in this problem, a is three digit and b is two digit, we set a=245 and b=96. Their difference is 149.
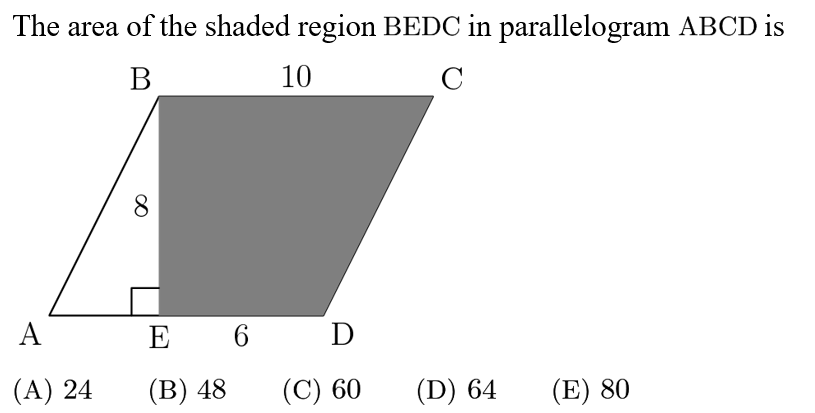
Answer: D
Solution:
Area of ABCD is 8*10=80; the area of triangle ABE=1/2 * (10-6)*8=16.
The shaded area is 80-16=64.

Answer: A
Solution:
For 47 to be written as the sum of two integers, one must be odd and the other must be even. There is only one even prime, namely 2, so one of the numbers must be 2, making the other 45. However, 45 is not prime, so there are no ways to write 47 as the sum of two primes .

Answer: B
Solution:
We know that 9<N<17 and we wish to bound (6+10+N)/3=(16+N)/3.
From what we know, we can deduce that 25<N+16<33, and thus 8.3<(N+16)/3 < 11. The only answer choice that falls in this range is B.

Answer: B
Solution:
X=1/(1/x); thus, we need to iterate the key pressing twice to get the display back to the original.


Answer: B
Solution:
Since we want to know how much money is spent in June, July and August, we need the difference between the amount of money spent by the beginning of June and the amount of money spent by the end of August. We estimate these to be about 2.2 million and 4.8 million, respectively. The difference is4.8-2.2=2.6=2.5

Answer: D
Solution:
It is clear that 6,5,and 4 will not come together to get a sum of 15. The faces 6, 5, and3 come together at a common vertex, making the maximal sum 6+5+3=14.

Answer: D
Solution:
128*3/4 * 3/4-1=71.

Answer: C
Solution:
Every 4th line has 1989 as part of it and every 6th line has AJHSMFA as part of it. In order for both to be part of line n, n must be a multiple of 4 and 6 the least of which is 12.
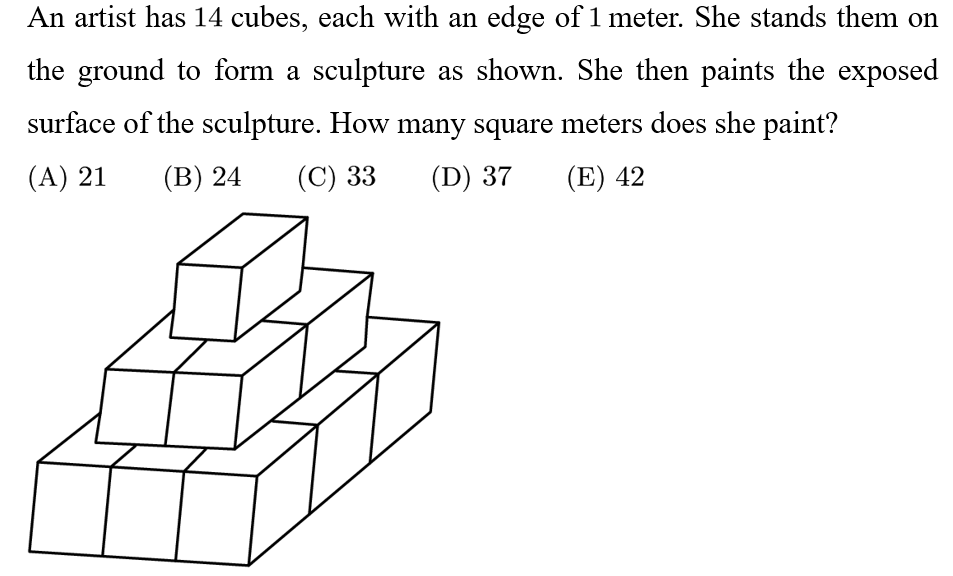
Answer: C
Solution:
We can consider the contributions of the sides of the three layers and the tops of the layers separately.
Layer n (counting from the top starting at 1) has 4 side faces each with n unit squares, so the sides of the pyramid contribute 4+8+12=24 for the surface area.
The tops of the layers when combined form the same arrangement of unit cubes as the bottom of the pyramid, which is a 3*3 square, hence this contributes 9 for the surface area.
Thus, the artist paints 24+9=33 square meters.

Answer: E
Solution:
the perimeter of one of the small rectangles is 2*(4x+x)=10x and the perimeter of the large rectangle is 2*(4x+2x)=12x . The desired ratio is 10x/12x=5/6.
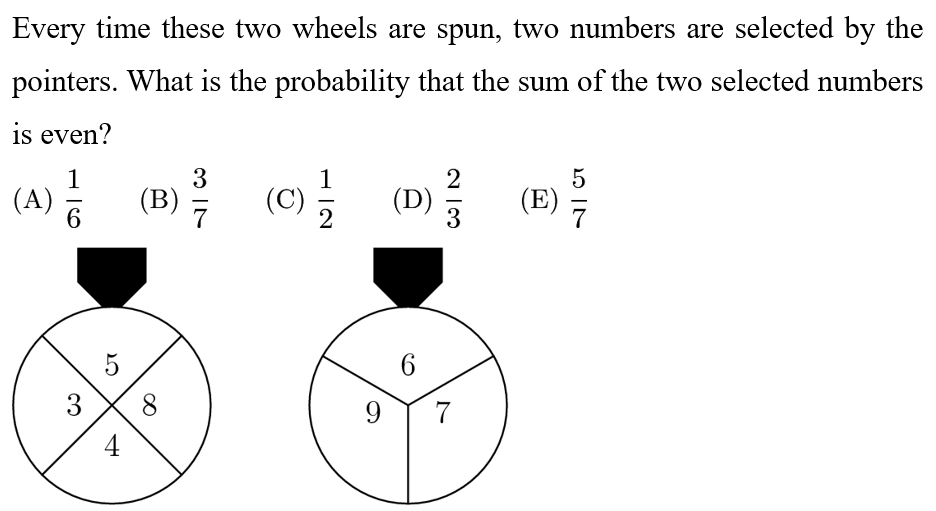
Answer: C
Solution:
For the sum to be even, the two selected numbers must have the same parity.The first spinner has 2 odd numbers and 2 even, so no matter what the second spinner is, there is a 1/2 chance the first spinner lands on a number with the same parity, so the probability of an even sum is 1/2.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,